¿Añadir más carriles mejora el tráfico?. No siempre: Paradoja de Braess.

A todos nos ha pasado, llegamos a las colas de varios carriles u opciones, y no sabemos donde colocarnos, ni cual será la más rápida; lo mismo que nos sucede en un supermercado y en otras circunstancias. Existe en matemáticas una parte que se dedica a estudiar estos procesos, explicarlos y tratar de optimizarlos, esta disciplina se llama Teoría de Colas, y sirve para que el tráfico en internet, las telecomunicaciones sean más rápidas, que las carreteras funcionen mejor, que cuando lleguemos a cualquier cola supermercados, aeropuertos y las fábricas, funcionen mejor,….

Debes saber también que estos fenómenos son cadenas de Markov, es decir procesos aleatorios estocásticos que varían con el tiempo, como lo hace el clima o los mercados de valores en bolsa,…. y no tienen memoria de lo que ha pasado anteriormente, porque lo que probablemente puede suceder ahora depende exclusivamente de la situación actual del sistema. Por eso tenemos que olvidarnos de lo que haya sucedido anteriormente a la hora de elegir la cola que creamos que es más rápida.

La paradoja de Braess dicta que al agregar mayor capacidad a una red, cuando los actores que transitan por ella escogen la ruta de forma egoísta, puede que en algunos casos reducir la fluidez de toda la red. El trabajo original de Braess mostraba una situación paradójica, en la que la construcción de una vía adicional (con la consecuente inversión de capital), llevaba a que, con la misma demanda de tráfico, los tiempos de viaje para todos los usuarios de la red aumentaran. Cuantos más automóviles usan una vía, más se reduce la velocidad de todos los vehículos que la usan y se llega a un mayor tiempo de viaje. Aquellas vías que tienen mayor capacidad (por ejemplo, más carriles para tráfico) podrán albergar más vehículos sin que la velocidad se vea afectada, mientras que vías con poca capacidad se congestionan más rápido.

La principal causa de los atascos es el egoísmo. Una velocidad excesiva, una velocidad anormalmente baja y los cambios de carril inadecuados se combinan para entorpecer el tráfico. El que va demasiado lento obliga a otros conductores a adelantar; el que va demasiado rápido trata de buscar hueco para seguir a su ritmo. En un mundo ideal, los conductores mantendrían una velocidad y distancia entre sí muy constantes y el tráfico fluiría. Por eso poner un carril más para mejorar el tráfico no es siempre efectivo, a veces empeora la situación, incluso con el mismo número de vehículos.  En supermercados conocidos y aeropuertos hay una sóla cola y la gente se va distribuyendo en las salidas que van quedando libres al llegar, distribuyendo los problemas de retrasos equitativamente y reduciendo el tiempo global de espera. Incluso en algunos casos eliminar un carril mejoraría la situación del tráfico, es increible pero cierto (paradógico), como ha ocurrido en ciudades como New York, Boston o London.

Los usuarios de las vías tienden a escoger la ruta que más les conviene individualmente (por eso se les llama usuarios “egoístas”) y esto implica que cada usuario tratará de buscar la ruta que le represente menores tiempos de viaje. Braess demostró con un ejemplo simple, cómo al agregar más vías en una red de tráfico, se puede llegar a empeorar el desempeño de todos los usuarios.

El diagrama 1 representa una red de carreteras en la que las vías secundarias se simbolizan en amarillo y las autovías en rojo.

DIAGRAMA 1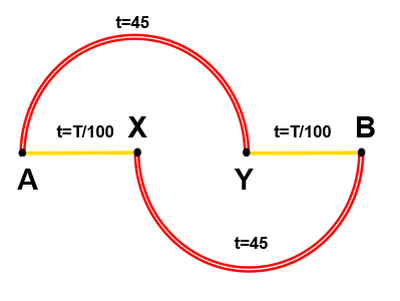

La velocidad del tráfico en los tramos de A a X y Y a B –las carreteras secundarias– depende fuertemente de la cantidad de vehículos que circulan por ellos; si T es el número de automóviles transitando, se sabe que cada viajero necesita t=T/100 minutos para realizar el recorrido completo.

Los trayectos de A a Y y de X a B requieren, cada uno de ellos, un tiempo constante de 45 minutos: son vías rápidas en las que el tráfico es siempre fluido, independientemente del número de vehículos circulando. Supongamos que 4000 conductores quieren viajar desde A hasta B. Las rutas por el norte (de A a Y y de Y a B) y por el sur (de A a X y de X a B) son igualmente eficientes, por lo que los viajeros se dividirán –si no intermedia ningún dato adicional– en dos grupos, y llegarán al final de su trayecto en 2000/100 + 45 = 65 minutos.

Imaginemos ahora que los responsables de tráfico, intentando reducir los tiempos de los viajes, agregan un acceso directo entre X e Y, cuyo recorrido precisa sólo 1 minuto (ver diagrama 2).

DIAGRAMA 2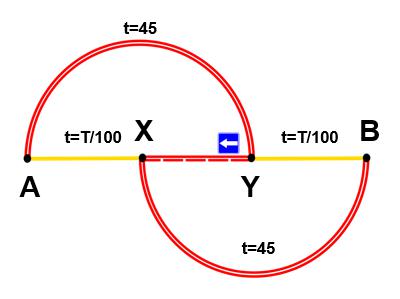

¿Cómo razonará ahora un viajero cualquiera? Tomará la ruta de A a X ya que, en el peor de los casos –si los demás argumentan de la misma manera– tardará 4000/100 = 40 minutos en llegar de A a X, en lugar de los 45 minutos que invertía con la primera ruta. Tras 1 minuto para llegar de X a Y, de nuevo en el peor de los casos, necesitará 4000/100 = 40 minutos para llegar de Y a B.

Es decir, el viaje le llevará 4000/100 + 1+ 4000/100 = 81 minutos… ¡16 minutos más que al principio, antes ‘de las mejoras’!

Ningún conductor –individualmente– tiene ningún incentivo para cambiar su manera de razonar y su comportamiento ulterior: de hecho, si todos los vehículos pudieran ponerse de algún modo de acuerdo para no usar el acceso directo recién añadido, todos reducirían su tiempo de viaje. Pero, sin una manera de coordinarlo, la ‘supuesta mejora’ sólo consigue desplazamientos más largos…

Vale la pena preguntarse si existe evidencia en el mundo real de redes de transporte que aumenten su eficacia al ser privadas de alguna vía que antes formaba parte de ellas. La cuestión en sí es difícil de responder, pues las redes de transporte humanas son claramente muy complejas y en general hay muchos factores responsables de la eficacia de la red.

Sin embargo ramas de las matemáticas como la teoría de grafos y la probabilidad ofrecen una respuesta a la pregunta; pues se puede evidenciar que en una red aleatoria dotada de ciertas funciones que modelen su tránsito, el mismo fenómeno se presenta al eliminar algunas vías.

Si consideraramos una red posible de tránsito y tomamos como modelo un grafo aleatorio, hecho esto se puede evidenciar que en general las condiciones de la red permiten que al eliminar vías la movilidad sea más eficiente.

Los grafos en si mismos constituyen una manera muy conveniente de modelar y representar redes (no solo de tránsito), de ahí que sea natural usarlos para ver si es posible encontrar ejemplos más generales y cercanos a la realidad donde se presente este comportamiento paradójico.

Si definimos la red como el grafo G = (V , E) con un vértice de salida s y otro de llegada t. Si llamamos el conjunto de los caminos simples que van de s a t como P (no vacío). Como, el flujo de la red, es un número no negativo. Para un flujo fijo se define el flujo del tránsito en un camino p ∈ P como f_p, y se dice que f_e = ∑ f_p (p∈P, e∈p) es la cantidad de tráfico que pasa por la arista e, en la ruta s-t. La cantidad de tráfico en toda la red se denomina la tasa de tráfico y se nota con una R y el flujo se dice factible si  ∑ f_p = R, (p∈P).

Modelamos la «congestión» de la red asignándole a cada arista e una función no negativa, continua y no decreciente llamada función de demora l_e que describe la congestión en la arista e como función de el flujo f_e la demora total de un s-t camino p con respecto al flujo f está dado, entonces por l_p(f) = ∑ l_e (f_e) (e∈e). Por último se define la tripla (G, r, l) como una instancia.

En teoría de juegos es bien conocido el concepto del Equilibrio de Nash, en este ámbito; y dado que la decisión de cada usuario al elegir una ruta es una decisión egoísta, podemos interpretar el equilibrio de Nash como una propiedad del flujo a través de la red.

Dado f un flujo factible para (G , r , l) se dice que este es un Nash-flujo o simplemente un equilibrio de Nash si para toda con p₁, p₂ € P con f_p1 >0, se cumple l_p1 (f)≤  l_p2 (f). O, en otras palabras todos los caminos tienden a tener la misma «demora», lo cual se puede evidenciar claramente en el ejemplo, pues pasado el tiempo los usuarios tenderán a escoger el camino que les permita llegar a todos lo más rápido posible, y por ende el tiempo que demoran todos en llegar desde el punto de salida al de llegada es el mismo. Además también se sabe que en una red en donde los usuarios pueden escoger su ruta de forma egoísta tiene un único equilibrio de Nash.

REFERENCIAS

How Closing Roads Could Speed Up Traffic – The Braess Paradox

Paradoja de Braess

¿Cuál es la fila más rápida del supermercado?

M. Beckmann, C.B. Mcguire, and C.B. Winsten. Studies in the Economics of transportation. Yale University Press, 1956.

Redes de carreteras y atascos: la paradoja de Braess